• 在 V2.0 基础上添加多通道 AFD （MAFD）方法：
  • Core AFD
    • 多通道 传统实现方法（慢速）
    • 多通道 快速实现方法（快速）
  • Unwinding AFD
    • 多通道 传统实现方法（慢速）
    • 多通道 快速实现方法（快速）

• 实现方式变更为基于类编程。为了方便管理，分解结果与分解函数全部存于一个变量中。
• 现在包含 AFD 方法：
  • Core AFD
    • 单通道 传统实现方法（慢速）
    • 单通道 快速实现方法（快速）
  • Unwinding AFD
    • 单通道 传统实现方法（慢速）
    • 单通道 快速实现方法（快速）
• 现在可以自己选择搜索字典的生成方式 或是 使用自己生成的搜索字典。
• 文档发布

一个用来学习与测试 SSVEP 识别算法的 Python 包。目标是让研究人员快速熟悉 SSVEP 信号和相关识别算法，并缩短准备时间来专注于改进算法。

• 统一 SSVEP 数据格式
• 提供一个标准的数据处理流程来实现公平的算法比较
• 提供 SSVEP 识别算法的 Python 实现

数据库：

• Benchmark Dataset
• BETA Dataset

SSVEP 识别算法：

• Standard canonical correlation analysis (sCCA) and filterbank CCA (FBCCA)
• Extended CCA (eCCA)
• Multi-stimulus CCA (ms-CCA)
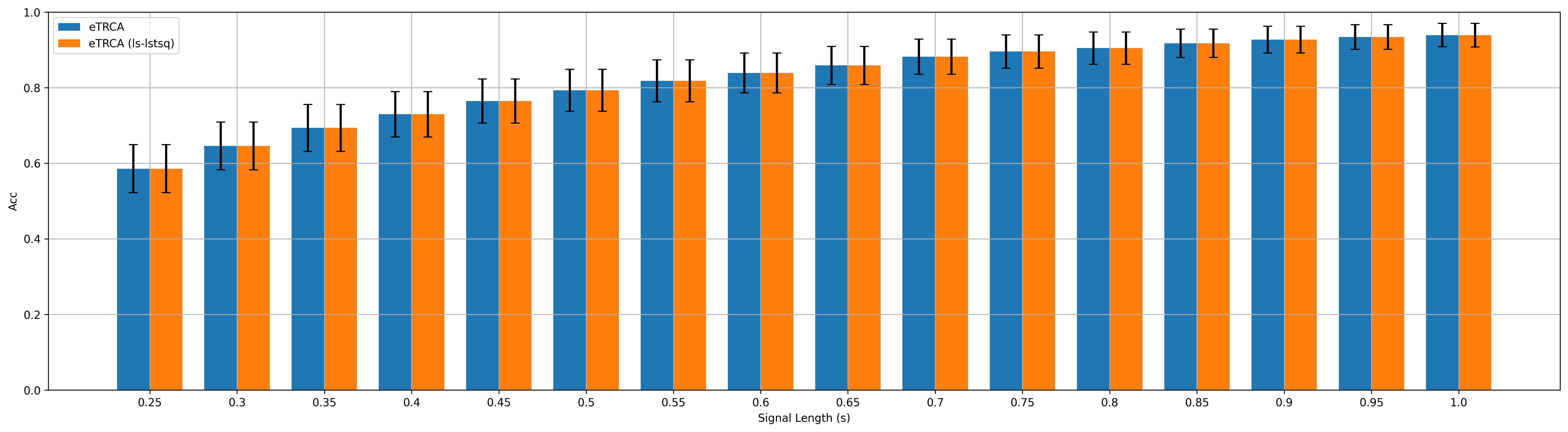
• Task-related component analysis (TRCA) and Ensemble TRCA (eTRCA)
• Multi-stimulus TRCA (ms-TRCA)
• Task-discriminant component analysis (TDCA)
• ...

This study is intended to achieve a general stimulus-stimulus transfer of SSVEP signals.

To achieve the stimulus-stimulus transfer, this study proposes a new perspective to analyze the SSVEP signals, which is the time-frequency-joint representation. In this representation, the SSVEP signals of different stimuli are synchronized according to the stimulus frequencies and phases. Then, the common components of different stimuli can be emphasied and become possible to be characterized and extracted. From the time-frequency-joint-representation point of view, a new SSVEP signal model is proposed for the stimulus-stimuls transfer. Moreover, an adaptive decomposition approach based on the multi-channel adaptive Fourier decomposition (MAFD) is designed to estimate components in the porposed SSVEP model, which is the MAFD with different phases (DP-MAFD).

Codes in this repository implement the simulations for the Benchmark Dataset. Simulation results show the classification performance of SSVEP templates constructed by the proposed stimulus-stimulus trnasfer.

Ze Wang et al., "Stimulus-stimulus transfer based on time-frequency-joint representation in SSVEP-based BCIs," IEEE Trans. Biomed. Eng., 2022. DOI: 10.1109/TBME.2022.3198639.

使用 Matlab 建立的一个 6 自由度 3D Yaskawa 模型演示。

此演示中包括两个 demo，一个是控制机器臂绘制 “UM” 字样，一个是控制控制机器臂绘制一个圆形。

使用 Matlab 建立的基于模糊控制的倒立摆。